| Date | May 2014 | Marks available | 2 | Reference code | 14M.1.sl.TZ1.13 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find | Question number | 13 | Adapted from | N/A |
Question
The graph of the quadratic function \(f(x) = a{x^2} + bx + c\) intersects the y-axis at point A (0, 5) and has its vertex at point B (4, 13).
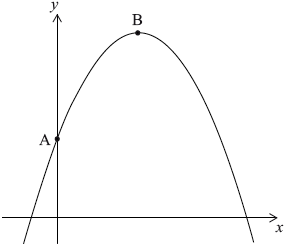
Write down the value of \(c\).
By using the coordinates of the vertex, B, or otherwise, write down two equations in \(a\) and \(b\).
Find the value of \(a\) and of \(b\).
Markscheme
5 (A1) (C1)
[1 mark]
at least one of the following equations required
\(a{(4)^2} + 4b + 5 = 13\)
\(4 = - \frac{b}{{2a}}\)
\(a{(8)^2} + 8b + 5 = 5\) (A2)(A1) (C3)
Note: Award (A2)(A0) for one correct equation, or its equivalent, and (C3) for any two correct equations.
Follow through from part (a).
The equation \(a{(0)^2} + b(0) = 5\) earns no marks.
[3 marks]
\(a = - \frac{1}{2},{\text{ }}b = 4\) (A1)(ft)(A1)(ft) (C2)
Note: Follow through from their equations in part (b), but only if their equations lead to unique solutions for \(a\) and \(b\).
[2 marks]

