| Date | November 2013 | Marks available | 2 | Reference code | 13N.1.sl.TZ0.12 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find | Question number | 12 | Adapted from | N/A |
Question
A quadratic function \(f:x \mapsto a{x^2} + b\), where \(a\) and \(b \in \mathbb{R}\) and \(x \geqslant 0\), is represented by the mapping diagram.
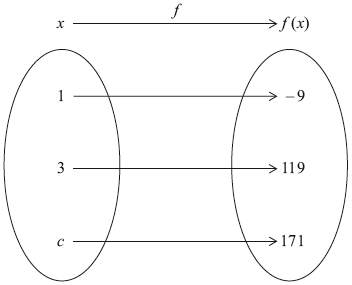
Using the mapping diagram, write down two equations in terms of \(a\) and \(b\).
Solve the equations to find the value of
(i) \(a\);
(ii) \(b\).
Find the value of \(c\).
Markscheme
\(a{(1)^2} + b = - 9\) (A1)
\(a{(3)^2} + b = 119\) (A1) (C2)
Note: Accept equivalent forms of the equations.
[2 marks]
(i) \(a = 16\) (A1)(ft)
(ii) \(b = - 25\) (A1)(ft) (C2)
Note: Follow through from part (a) irrespective of whether working is seen.
If working is seen follow through from part (i) to part (ii).
[2 marks]
\(16{c^2} - 25 = 171\) (M1)
Note: Award (M1) for correct quadratic with their \(a\) and \(b\) substituted.
\(c = 3.5\) (A1)(ft) (C2)
Note: Accept \(x\) instead of \(c\).
Follow through from part (b).
Award (A1) only, for an answer of \( \pm 3.5\) with or without working.
[2 marks]
Examiners report
This question was answered reasonably well with many candidates able to write down the two equations and solve them for a and b. Errors such as mistaking the equation given for \(3{a^2} + b = 119\) meant that marks were lost even though the candidates appeared to know what they needed to do. Most candidates who were able to set up the equation in part (c) solved it correctly. Follow through marks were awarded to many candidates for correct working with their substituted values from part (b).
This question was answered reasonably well with many candidates able to write down the two equations and solve them for a and b. Errors such as mistaking the equation given for \(3{a^2} + b = 119\) meant that marks were lost even though the candidates appeared to know what they needed to do. Most candidates who were able to set up the equation in part (c) solved it correctly. Follow through marks were awarded to many candidates for correct working with their substituted values from part (b).
This question was answered reasonably well with many candidates able to write down the two equations and solve them for a and b. Errors such as mistaking the equation given for \(3{a^2} + b = 119\) meant that marks were lost even though the candidates appeared to know what they needed to do. Most candidates who were able to set up the equation in part (c) solved it correctly. Follow through marks were awarded to many candidates for correct working with their substituted values from part (b).

