| Date | May 2014 | Marks available | 2 | Reference code | 14M.1.sl.TZ2.6 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Hence | Question number | 6 | Adapted from | N/A |
Question
The surface of a red carpet is shown below. The dimensions of the carpet are in metres.
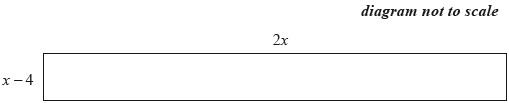
Write down an expression for the area, \(A\), in \({{\text{m}}^2}\), of the carpet.
The area of the carpet is \({\text{10 }}{{\text{m}}^2}\).
Calculate the value of \(x\).
The area of the carpet is \({\text{10 }}{{\text{m}}^2}\).
Hence, write down the value of the length and of the width of the carpet, in metres.
Markscheme
\(2x(x - 4)\) or \(2{x^2} - 8x\) (A1) (C1)
Note: Award (A0) for \(x - 4 \times 2x\).
[1 mark]
\(2x(x - 4) = 10\) (M1)
Note: Award (M1) for equating their answer in part (a) to \(10\).
\({x^2} - 4x - 5 = 0\) (M1)
OR
Sketch of \(y = 2{x^2} - 8x\) and \(y = 10\) (M1)
OR
Using GDC solver \(x = 5\) and \(x = - 1\) (M1)
OR
\(2(x + 1)(x - 5)\) (M1)
\(x = 5{\text{ (m)}}\) (A1)(ft) (C3)
Notes: Follow through from their answer to part (a).
Award at most (M1)(M1)(A0) if both \(5\) and \(-1\) are given as final answer.
Final (A1)(ft) is awarded for choosing only the positive solution(s).
[3 marks]
\(2 \times 5 = 10{\text{ (m)}}\) (A1)(ft)
\(5 - 4 = 1{\text{ (m)}}\) (A1)(ft) (C2)
Note: Follow through from their answer to part (b).
Do not accept negative answers.
[2 marks]

