| Date | November 2017 | Marks available | 3 | Reference code | 17N.1.sl.TZ0.1 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Draw | Question number | 1 | Adapted from | N/A |
Question
A group of 20 students travelled to a gymnastics tournament together. Their ages, in years, are given in the following table.
The lower quartile of the ages is 16 and the upper quartile is 18.5.
For the students in this group find the mean age;
For the students in this group write down the median age.
Draw a box-and-whisker diagram, for these students’ ages, on the following grid.
Markscheme
\(\frac{{14 + 2 \times 15 + 7 \times 16 + 17 + 4 \times 18 + 19 + 20 + 3 \times 22}}{{20}}\) (M1)
Note: Award (M1) for correct substitutions into mean formula.
\(( = ){\text{ }}17.5\) (A1) (C2)
[2 marks]
16.5 (A1) (C1)
[1 mark]
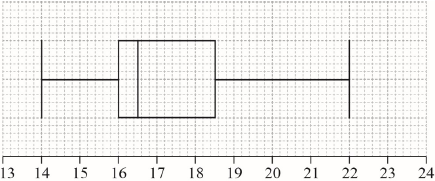(A1)(A1)(A1)(ft) (C3)
Note: Award (A1) for correct endpoints, (A1) for correct quartiles, (A1)(ft) for their median. Follow through from part (a)(ii), but only if median is between 16 and 18.5. If a horizontal line goes through the box, award at most (A1)(A1)(A0). Award at most (A0)(A1)(A1) if a ruler has not been used.
[3 marks]
