| Date | May 2008 | Marks available | 3 | Reference code | 08M.1.sl.TZ2.10 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Show that | Question number | 10 | Adapted from | N/A |
Question
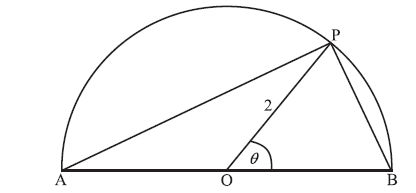
The following diagram shows a semicircle centre O, diameter [AB], with radius 2.
Let P be a point on the circumference, with \({\rm{P}}\widehat {\rm{O}}{\rm{B}} = \theta \) radians.
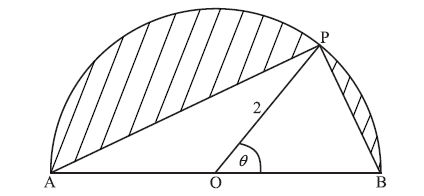
Let S be the total area of the two segments shaded in the diagram below.
Find the area of the triangle OPB, in terms of \(\theta \) .
Explain why the area of triangle OPA is the same as the area triangle OPB.
Show that \(S = 2(\pi - 2\sin \theta )\) .
Find the value of \(\theta \) when S is a local minimum, justifying that it is a minimum.
Find a value of \(\theta \) for which S has its greatest value.
Markscheme
evidence of using area of a triangle (M1)
e.g. \(A = \frac{1}{2} \times 2 \times 2 \times \sin \theta \)
\(A = 2\sin \theta \) A1 N2
[2 marks]
METHOD 1
\({\rm{P}}\widehat {\rm{O}}{\rm{A = }}\pi - \theta \) (A1)
\({\text{area }}\Delta {\rm{OPA}} = \frac{1}{2}2 \times 2 \times \sin (\pi - \theta )\) \(( = 2\sin (\pi - \theta ))\) A1
since \(\sin (\pi - \theta ) = \sin \theta \) R1
then both triangles have the same area AG N0
METHOD 2
triangle OPA has the same height and the same base as triangle OPB R3
then both triangles have the same area AG N0
[3 marks]
area semicircle \( = \frac{1}{2} \times \pi {(2)^2}\) \(( = 2\pi )\) A1
\({\text{area }}\Delta {\rm{APB}} = 2\sin \theta + 2\sin \theta \) \(( = 4\sin \theta )\) A1
\(S{\text{ = area of semicircle}} - {\text{area }}\Delta {\rm{APB}}\) \(( = 2\pi - 4\sin \theta )\) M1
\(S = 2(\pi - 2\sin \theta )\) AG N0
[3 marks]
METHOD 1
attempt to differentiate (M1)
e.g. \(\frac{{{\rm{d}}S}}{{{\rm{d}}\theta }} = - 4\cos \theta \)
setting derivative equal to 0 (M1)
correct equation A1
e.g. \( - 4\cos \theta = 0\) , \(\cos \theta = 0\) , \(4\cos \theta = 0\)
\(\theta = \frac{\pi }{2}\) A1 N3
EITHER
evidence of using second derivative (M1)
\(S''(\theta ) = 4\sin \theta \) A1
\(S''\left( {\frac{\pi }{2}} \right) = 4\) A1
it is a minimum because \(S''\left( {\frac{\pi }{2}} \right) > 0\) R1 N0
OR
evidence of using first derivative (M1)
for \(\theta < \frac{\pi }{2},S'(\theta ) < 0\) (may use diagram) A1
for \(\theta > \frac{\pi }{2},S'(\theta ) > 0\) (may use diagram) A1
it is a minimum since the derivative goes from negative to positive R1 N0
METHOD 2
\(2\pi - 4\sin \theta \) is minimum when \(4\sin \theta \) is a maximum R3
\(4\sin \theta \) is a maximum when \(\sin \theta = 1\) (A2)
\(\theta = \frac{\pi }{2}\) A3 N3
[8 marks]
S is greatest when \(4\sin \theta \) is smallest (or equivalent) (R1)
\(\theta = 0\) (or \(\pi \) ) A1 N2
[2 marks]
Examiners report
Most candidates could obtain the area of triangle OPB as equal to \(2\sin \theta \) , though \(2\theta \) was given quite often as the area.
A minority recognized the equality of the sines of supplementary angles and the term complementary was frequently used instead of supplementary. Only a handful of candidates used the simple equal base and altitude argument.
Many candidates seemed to see why \(S = 2(\pi - 2\sin \theta )\) but the arguments presented for showing why this result was true were not very convincing in many cases. Explicit evidence of why the area of the semicircle was \(2\pi \) was often missing as was an explanation for \(2(2\sin \theta )\) and for subtraction.
Only a small number of candidates recognized the fact S would be minimum when sin was maximum, leading to a simple non-calculus solution. Those who chose the calculus route often had difficulty finding the derivative of S, failing in a significant number of cases to recognize that the derivative of a constant is 0, and also going through painstaking application of the product rule to find the simple derivative. When it came to justify a minimum, there was evidence in some cases of using some form of valid test, but explanation of the test being used was generally poor.
Candidates who answered part (d) correctly generally did well in part (e) as well, though answers outside the domain of \(\theta \) were frequently seen.

