| Date | November 2013 | Marks available | [N/A] | Reference code | 13N.2.sl.TZ0.7 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find, Hence, and Write down | Question number | 7 | Adapted from | N/A |
Question
Consider the graph of the semicircle given by \(f(x) = \sqrt {6x - {x^2}} \), for \(0 \leqslant x \leqslant 6\). A rectangle \(\rm{PQRS}\) is drawn with upper vertices \(\rm{R}\) and \(\rm{S}\) on the graph of \(f\), and \(\rm{PQ}\) on the \(x\)-axis, as shown in the following diagram.
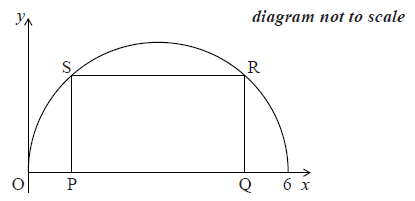
Let \({\text{OP}} = x\).
(i) Find \({\text{PQ}}\), giving your answer in terms of \(x\).
(ii) Hence, write down an expression for the area of the rectangle, giving your answer in terms of \(x\).
Find the rate of change of area when \(x = 2\).
The area is decreasing for \(a < x < b\). Find the value of \(a\) and of \(b\).
Markscheme
(i) valid approach (may be seen on diagram) (M1)
eg \({\text{Q}}\) to \(6\) is \(x\)
\({\text{PQ}} = 6 - 2x\) A1 N2
(ii) \(A = (6 - 2x)\sqrt {6x - {x^2}} \) A1 N1
[3 marks]
recognising \(\frac{{{\text{d}}A}}{{{\text{d}}x}}\) at \(x = 2\) needed (must be the derivative of area) (M1)
\(\frac{{{\text{d}}A}}{{{\text{d}}x}} = - \frac{{7\sqrt 2 }}{2},{\text{ }} - 4.95\) A1 N2
[2 marks]
\(a = 0.879{\text{ }}b = 3\) A1A1 N2
[4 marks]

